Démonstration expérimentale de l’équation de Boltzmann

Appliquons le principe de pire action.

Utilisons une tuyère supersonique A ; la méthode des caractéristiques permet de définir l’état du gaz en chaque point. Le nombre des caractéristiques peut être très grand, et donc le réseau beaucoup plus fin que celui présenté. Dans la zone de détente, les propriétés de l’écoulement (vitesse, direction de la vitesse, température statique, etc.) sont notablement différentes entre des points quelconques 1 et 2.

Prenons une autre tuyère supersonique B, analogue aux tuyères propulsives des fusées spatiales, fonctionnant entre les mêmes nombres de Mach que la précédente.

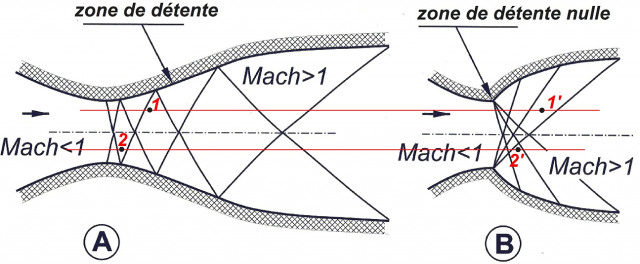
villani3Complet

Entre les points 1 et 1′ (ou 2 et 2′) correspondants des deux tuyères, les diverses propriétés du fluide sont évidemment différentes.
Construisons maintenant une structure sandwich, dotée d’une certaine épaisseur, en utilisant ces deux tuyères. Avec une telle stratification, tout change. L’écoulement se morcelle en un nombre immense de complexions W. Chacune des innombrables particules est entourée de particules dont les vitesses, directions des vitesses, etc. sont différentes de la sienne.

Dans cette utilisation curieuse des écoulements supersoniques, deux écoulements initialement presque réversibles conduisent quasi-instantanément à une augmentation abondante d’entropie. Ce qui pourrait être considéré comme une démonstration expérimentale de la formule de Boltzmann.
Appliquons enfin ce procédé, dénommé vistemboir, à une maquette de soupape de régulation. Dans certaines situations réelles de marche, des dizaines de mégawatts doivent être dégradées. La confrontation entre la version de référence A (issue d’un consensus entre les industriels français et EDF) et la version B munie de vistemboirs donne des résultats remarquables, et ceci dès le premier essai. Un expérimentateur qui tombe (pour l’unique fois de sa vie) sur un résultat aussi flagrant en reste interloqué. Ce constat éclatant devrait encore faire progresser les idées de Boltzmann en énergétique.

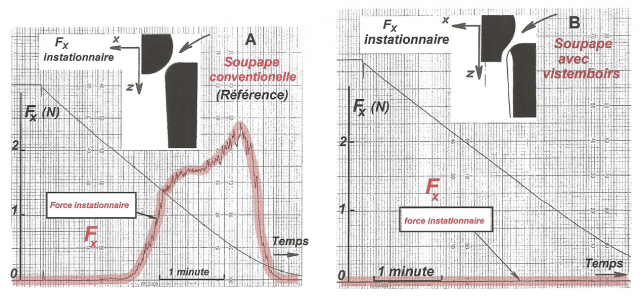
VillaniFig5Complet

– Dans le premier cas A, le fluide a toute la liberté pour dissiper lui-même son énergie cinétique. Alors on pénètre dans le chaos, puis apparaissent les structures dissipatives de Prigogine, qui font généralement l’admiration des hommes mais qui peuvent devenir très dangereuses dans les soupapes et dans d’autres applications en énergétique.
– Dans le second cas B, on impose au système moléculaire de rejoindre immédiatement le point d’équilibre final, grâce à la géométrie utilisée. Des phénomènes de transport encore inconnus créent une intense dégradation de l’énergie. Le nombre faramineux de complexions engendre énormément d’entropie et épuise la puissance cinétique contenue dans le fluide. Toutes les caractéristiques instationnaires de l’écoulement sont anéanties.

Conclusion : en introduisant un désordre massif dans le monde microscopique, on évite le chaos dans notre monde macroscopique. L’application du principe de pire action permet une dégradation quasi-immédiate de l’énergie cinétique des jets supersoniques dans une soupape.

Au sujet de l'auteur Michel Pluviose

Michel Pluviose, Ingénieur, docteur d’état ès sciences, professeur honoraire du Conservatoire national des Arts et Métiers (CNAM), a été titulaire de la chaire de turbomachines, et : - Directeur du laboratoire de l’ATTAG (Association Technique pour les Turbomachines et turbines à Gaz), - Responsable des activités "fluides compressibles" au CETIM (Centre Technique des Industries Mécaniques), - Scientifique de haut niveau mais aussi homme de terrain, il a été ingénieur chez Hispano-Suiza, à la SNECMA, - Responsable du traité "Machines hydrauliques et thermiques" aux Techniques de l'Ingénieur.

Démonstration expérimentale de l’équation de Boltzmann

Appliquons le principe de pire action.

Au sujet de l'auteur Michel Pluviose

Articles similaires

Laisser un commentaire